Wichtige kryptographische Begriffe und Konzepte

vom 26.03.2018

---

Inhaltsverzeichnis

• Was ist Kryptologie?
• Anforderungen an kryptographische Systeme
• Weitere Begriffe
  • Datenschutz und Datensicherheit
    • Datenschutz
    • Datensicherheit
• Klartext und Chiffrierung
• Grundlegendes Szenario
• Probleme bei symmetrischen Verfahren
• Asymmetrische Verfahren
• Block- und Strom-Chiffren
• Grundsätzliche kryptographische Operationen
• Kerckhoff'sches Prinzip
• Monoalphabetische Chiffren
  • Shift-Chiffre
  • Affine Chiffre
• Polyalphabetische Chiffren
  • Die Vigenére-Chiffre
  • Die HILL-Chiffre
• Eigenschaften von Block-Chiffren
• Mathematische Grundlagen (kurz)
  • Relativ prime Zahlen
  • Totientenfunktion
  • Kleiner Satz von FERMAT
• RSA-Algorithmus
• DIFFIE-HELLMAN Key-Exchange Verfahren
  • Das DH-Key-Exchange Kryptosystem
• ELGAMAL-Kryptosysteme (TAHER ELGAMAL, 1985)
  • Digitale Signatur
• Die FEISTEL-Chiffre
• Betriebsmodi von Block-Chiffren
  • Electronic Code Book Mode (ECB)
  • Cipher Block Chaining Mode (CBC)

Was ist Kryptologie?

Kryptologie ist eine Wissenschaft, die sich mit Methoden der Verschlüsselung und damit verwandten Verfahren befasst. Kryptologen sind ausgebildete High-End-Mathematiker.

Kryptographie bezeichnet den Zweig der Kryptologie, der sich mit der Erstellung und dem Design kryptographischer Algorithmen befasst. In der Kryptoanalyse geht es um das nicht-autorisierte Brechen der Verschlüsselungen.

Der Kryptologie liegt ein einfaches Kommunikationsmodell zugrunde:

Alice und Bob wollen vertraulich kommunizieren, d.h. eine Nachricht, die Alice sendet, soll nur von Bob gelesen werden können (und umgekehrt).

Ein Angreifer heißt in diesem Modell Eve, deren Ziel es ist, die Kommunikation zu beeinflussen.

Anforderungen an kryptographische Systeme

Bei der Kryptographie geht es um folgende wesentliche Punkte:

• Geheimhaltung
  • Ein kryptographisches System, das Geheimhaltung gewährleistet, verhindert die Entnahme von Informationen durch eine dritte, nicht autorisierte Partei während der Übertragung über einen unsicheren Kommunikationskanal.
  • Oder: Der Sender einer Nachricht kann sicher sein, dass nur der legitime Empfänger die Nachricht lesen kann.
• Authentizität
  • Ein kryptographisches System, das Authentizität gewährleistet, verhindert das nicht autorisierte Einschleusen einer Nachricht in einen unsicheren Kommunikationskanal.
  • Oder: Der Empfänger kann sicher sein, dass die Nachricht vom angegebenen Sender stammt.
• Digitale Signatur
  • Der Empfänger einer Nachricht kann eine neutrale Partei davon überzeugen, wer die Nachricht verfasst hat (ist schärfer als Authentifikation)
• Integrität
  • Ein kryptographisches System, das Integrität gewährleistet, verhindert die nicht autorisierte Manipulation des Inhalts einer Nachricht während der Übertragung über einen unsicheren Kommunikationskanal.
• Verbindlichkeit
  • Sender und Empfänger soll es nicht möglich sein, im Nachhinein zu behaupten, die Nachricht nicht gesendet / empfangen zu haben (ist so ähnlich wie ein Einschreiben).

Weitere Begriffe

• Identifikation
  • bedeutet die eindeutige Zuordnung einer Identität zu einem Subjekt, z.B. Benutzername / E-Mail
• Authentifizierung
  • Verifikation der Gültigkeit einer Tatsache (Passwort / PIN)
• Autorisierung
  • Zuordnung von Rechten zu einem Subjekt

Vorstellbare Klausuraufgaben:

• Stellen Sie den Unterschied zwischen Authentifizierung und Autorisierung heraus.
  • Antwort: Bei der Authentifizierung geht es um den Beweis der eigenen Identität, in der Regel ein Anmeldeprozess. Bei der Autorisierung hingegen berechtigt man eine dritte Person, die Nachricht zu lesen. Übertagen auf die Kryptographie bedeutet dies, dass die Authentifizierung sicherstellt, dass nur der legitime Empfänger einer Nachricht diese auch lesen kann. Bei der Autorisierung berechtigt man eine dritte Partei, die Nachricht auch zu lesen.
• Was grenzt den Datenschutz von der Datensicherheit ab (siehe Begriffe im Folgenden definiert)?
  • Antwort: Der Datenschutz regelt, in welchem Maße personenbezogene Daten überhaupt erhoben werden dürfen, wer diese sehen und abrufen kann und wer damit “handeln” darf. Er zeigt Richtlinien für den Umgang mit diesen Daten auf. Die Datensicherheit beschäftigt sich mit der Privatisierung bzw. dem allgemeinen Schutz von Daten, die bereits erhoben wurden.

Datenschutz und Datensicherheit

Datenschutz

“Je nach Betrachtungsweise wird Datenschutz verstanden als Schutz vor missbräuchlicher Datenverarbeitung, Schutz des Rechts auf informationelle Selbstbestimmung, Schutz des Persönlichkeitsrechts bei der Datenverarbeitung und auch Schutz der Privatsphäre.”

Definition Datenschutz von Wikipedia (Quelle)

Der Datenschutz behandelt den Umgang mit personenbezogenen Daten. Hier geht es um die Frage, ob personenbezogene Daten überhaupt erhoben werden dürfen und / oder verarbeitet / anonymisiert werden.

Datensicherheit

“Als Informationssicherheit bezeichnet man Eigenschaften von informationsverarbeitenden und -lagernden (technischen oder nicht-technischen) Systemen, die die Schutzziele Vertraulichkeit, Verfügbarkeit und Integrität sicherstellen. Informationssicherheit dient dem Schutz vor Gefahren bzw. Bedrohungen, der Vermeidung von wirtschaftlichen Schäden und der Minimierung von Risiken.”

Definition Datensicherheit von Wikipedia (Quelle)

Datensicherheit versucht, die schon vorhandenen Daten (ob personenbezogen oder nicht) in einem informationstechnischen System zu schützen / unzugänglich zu machen.

Klartext und Chiffrierung

Definition: Der Klartext (engl. cleartext oder plaintext) ist die Nachricht, die durch ein geeignetes Verfahren in eine Form transformiert wird, dass eine Informationsentnahme durch eine dritte Partei nicht möglich ist.

Es gibt zwei grundlegende Verfahren, eine Nachricht vor Informationsentnahme zu schützen:

• Kryptographische Verfahren (“unlesbar machen”)
• Steganographie (Existenz der Nachricht verschleiern)

Das Verfahren, einen Klartext in eine Form zu transformieren, dass die Informationsentnahme nicht möglich ist, heißt Verschlüsselung oder Chiffrierung. Eine verschlüsselte Nachricht heißt Chiffretext.

Anmerkung: Kodierung hat eine andere Bedeutung, nämlich Umwandlung in eine andere Form, damit sie geeignet verarbeitet werden kann.

Die Umkehrung heißt Entschlüsselung oder Dechiffrierung.

Üblicherweise verwenden heutige kryptographische Verfahren einen Schlüssel $K$, das ist ein besonderer Wert aus einem Schlüsselraum.

Grundlegendes Szenario

Sender und Empfänger benötigen den gleichen Schlüssel $K$ zum Ver- / Entschlüsseln (daher symmetrische Verschlüsselung).

Probleme bei symmetrischen Verfahren

Symmetrische Systeme haben (alle) drei grundsätzliche Probleme:

1. Key Exchange Problem
   • Der Schlüssel $K$ muss auf sicherem Weg von Alice zu Bob gelangen.
2. Key Management Problem
   • Bei $n$ Parteien: Wieviele $K$s werden benötigt?
   • $\rightarrow \frac{n (n - 1)}{2}$
   • Wird für jede Sitzung ein eigener Schlüssel verwendet oder für alle der Gleiche?
3. Mit symmetrischen Verfahren ist es nicht möglich, eine digitale Signatur zu realisieren. Es gibt kein eindeutiges Identifikationsmerkmal für den Sender einer Nachricht.

Asymmetrische Verfahren

Public-Key Kryptographie oder asymmetrische Verschlüsselung

Das funktioniert so:

Szenario 1: Alice will Bob eine vertrauliche Nachricht zukommen lassen (ohne Key-Exchange)

1. Bob erzeugt zwei Schlüssel $K_{\text{priv}}$ und $K_{\text{pub}}$
   • $K_{\overset{B}{\text{priv}}}$ ist nur Bob bekannt.
   • $K_{\overset{B}{\text{pub}}}$ kann veröffentlicht werden.
2. Alice besorgt sich $K_{\overset{B}{\text{pub}}}$ von Bob.
3. Alice verschlüsselt den Klartext mit Bobs $K_{\overset{B}{\text{pub}}}$.
   • $\rightarrow$ Chiffretext
4. Chiffretext geht an Bob (Bedingung: $D_{K_{\overset{B}{\text{pub}}}} (E_{K_{\overset{B}{\text{pub}}}} (M)) \ne M$
   • Die Entschlüsselung darf mit dem Public-Key von Bob nicht möglich sein.
5. Bob entschlüsselt das Chiffrat mit seinem $K_{\overset{B}{\text{priv}}}$, den nur er hat
   • $\rightarrow$ Klartext

$D_{K_{\overset{B}{\text{priv}}}} (E_{K_{\overset{B}{\text{pub}}}} (M)) = M$

Nur mit dem privaten Schlüssel $K_{\overset{B}{\text{priv}}}$ von Bob darf die Entschlüsselung möglich sein.

Somit ist das Key-Exchange Problem gelöst, da ein Schlüssel ausreicht ($K_{\overset{B}{\text{pub}}}$), mit dem beliebig viele Parteien vertraulich mit Bob kommunizieren können.

In der Praxis: Public-Key-Verfahren sind etwa 1000x langsamer als symmetrische Verfahren.

Man verwendet daher sogenannte Hybrid-Verfahren.

Die Public-Key-Verfahren werden dabei genutzt, um zwischen Sender und Empfänger einen Sitzungsschlüssel auszutauschen; die Nutzdaten werden dann symmetrisch verschlüsselt, da Sender und Empfänger einen gemeinsamen Schlüssel haben.

Szenario 2: Digitale Signatur, Alice will Bob ein signiertes Dokument zukommen lassen.

1. Alice erzeugt ein Schlüsselpaar ($K_{\overset{A}{\text{priv}}}, K_{\overset{A}{\text{pub}}}$) (Sender).
2. Alice verschlüsselt den Klartext mit ihrem $K_{\overset{A}{\text{priv}}}$ (den nur Alice hat)
   • $\rightarrow$ Chiffrat
   • Idee: $D_{K_{\overset{A}{\text{pub}}}} (E_{K_{\overset{A}{\text{priv}}}} (M)) = M$
3. Chiffrat geht an Bob.
4. Bob besorgt sich $K_{\overset{A}{\text{pub}}}$ und dechiffriert das erhaltene Chiffrat.
5. Entsteht Klartext, dann ist auch für eine neutrale dritte Partei gezeigt, dass Alice die Nachricht verfasst hat.

In der Praxis geht das etwas anders:

Der Hash-Algorithmus erzeugt eine Prüfziffer ($180$ Bit), die klartext-abhängig ist und sich ändert, falls die Nachricht manipuliert wurde. Damit garantiert der Hashwert die Integrität, d.h. das ist das Instrument, um zu prüfen, ob der Klartext während der Übertragung manipuliert wurde.

Block- und Strom-Chiffren

Sowohl symmetrische als auch asymmetrische Verfahren können in Form von Block-Chiffre oder Strom-Chiffre eingesetzt werden.

Bei Block-Chiffren werden Bitblöcke, z.B. $64$-Bit, in einem Vorgang in einen $64$-Bit Chiffreblock verschlüsselt (Klartext $\rightarrow$ aufteilen in $n$ $64$-Bit Blöcke).

Bei Strom-Chiffren (bspw. bei WLAN) wird Zeichen für Zeichen verschlüsselt (bit- / byteweise).

Grundsätzliche kryptographische Operationen

Es gibt in den meisten kryptographischen Systemen zwei grundsätzliche Operationen, wie Klartext in Chiffretext transformiert wird.

• Substitution
  • Bei einer Substitutionsoperation wird ein Klartextzeichen (oder ein Klartextblock) durch ein anderes Zeichen ersetzt. Die Position des Zeichens / Blocks bleibt erhalten.
• Transposition (auch Permutation oder Vertauschung)
  • Transpositionsoperationen vertauschen die Reihenfolge der Zeichen, d.h. die Positionen der Klartextzeichen innerhalb des Textes. Die Form bleibt erhalten.

Moderne Verfahren benutzen eine Vielzahl von Substitutions- bzw. Transpositionsoperationen.

---

Kerckhoff’sches Prinzip

In der Kryptographie wird in der Regel streng auf das KERCKHOFFs-Prinzip geachtet (1883).

Die Sicherheit eines Kryptosystems darf niemals von der Geheimhaltung des Verschlüsselungsalgorithmus abhängen, sondern ausschließlich von der Geheimhaltung des Schlüssels.

Monoalphabetische Chiffren

Shift-Chiffre

• Buchstaben des Klartextes werden um ein $k \in \mathbb{Z}_{26}$ verschoben
• Anmerkungen: $k = 3$ heißt üblicherweise CÄSAR-Chiffre

Die Shift-Chiffre ist eine sogenannte monoalphabetische Chiffre, d.h. das Klartextalphabet wird genau auf ein Chiffretextalphabet abgebildet. Dies hat zur Folge, dass die statistische Struktur des Klartextes erhalten bleibt.

Affine Chiffre

Definition: Sei $\{M\} = \{C\} = \mathbb{Z}_{26}$ und $\{K\} = \{(\alpha, \beta ) \in \mathbb{Z}_{26} \times \mathbb{Z}_{26} \ | \ \text{ggT}(\alpha, 26) = 1\}$.

Verschlüsselung:
$A_{(\alpha, \beta)}: \mathbb{Z}_{26} \rightarrow \mathbb{Z}_{26}$
$x \mapsto y = A_{(\alpha, \beta)}(x)$
$\qquad \quad = (\alpha \cdot x + \beta) \mod{26}$

Die Entschlüsselung ist:
$A_{(\alpha, \beta)}^{-1}: \mathbb{Z}_{26} \times \mathbb{Z}_{26}$
$y \mapsto x = A_{(\alpha, \beta)}^{-1}(y) \quad \text{mit Klartextzeichen} \ x$
$\qquad \quad = (\alpha^{-1} (y - \beta)) \mod 26$

mit $\alpha^{-1} \cdot \alpha \equiv 1 \mod 26$.

Anmerkungen:

1. Die Shift-Chiffre ist in der affinen Chiffre enthalten.
2. Schlüsselraum: Es gibt $12 \cdot 26 = 312$ verschiedene Schlüssel, da $\phi(26) = 12$.
3. Monoalphabetisch $\rightarrow$ Statistische Struktur bleibt erhalten.

Polyalphabetische Chiffren

Die Vigenére-Chiffre

Die Shift- und die affine Chiffre sind Beispiele von monoalphabetischen Chiffren, d.h. mit der Wahl eines Schlüssels wird jedes Klartextzeichen auf genau ein Chiffretextzeichen abgebildet (Eigenschaft, dass die statistische Struktur des Klartextes auf den Chiffretext übertragen wird).

Die Vigenére-Chiffre (1586 veröffentlicht) galt lange als nicht brechbar, bis in den 1860er Jahren Friedrich Kasicki und Charles Babbage daherkamen.

Definition: Sei $m$ eine positive ganze Zahl und
$M = C = K = (\mathbb{Z}_{26})^m = \mathbb{Z}_{26} \times \mathbb{Z}_{26} \times \ldots \times \mathbb{Z}_{26}$

Für einen festen Schlüsselwert $\vec{K} = (K_1, \ldots, K_m)$ ist
$V_k: \mathbb{Z}_{26} \rightarrow \mathbb{Z}_{26}$

$x \mapsto V_k(\vec{x})$

Dechiffrierung:
$V_k^{-1}: \mathbb{Z}_{26} \rightarrow \mathbb{Z}_{26}$
$y \mapsto (\vec{x} - \vec{k}) \mod 26$
$\quad \quad = [(x_1 - k_1) \mod 26, \ldots, (x_m - k_m) \mod 26]$.

Entschlüsselung: Mit dem gleichen Schlüsselwort einfach abziehen
$\rightarrow (x_i - k_i) \mod 26$

Schlüsselraum: $|K| = 26 \cdot 26 \cdot \ldots \cdot 26 = 26^m$ mit $\vec{k} = (k_1, k_2, \ldots, k_m)$.

Die Vigenére-Chiffre ist eine polyalphabetische Chiffre, weil durch die Wahl des Schlüssels $\vec{k} = (k_1, k_2, \ldots, k_m)$ (ohne Buchstabenwiederholung) ein Klartextzeichen auf $m$ mögliche Chiffrezeichen abgebildet wird.

Die HILL-Chiffre

1. Auswahl eines Schlüssels
   • Wähle eine Zahl, z.B. $k = 3;$ der Schlüssel ist eine $n \times m$-Matrix $M$, deren Einträge Zahlen $\mod 26$ sind.
2. Verschlüsselung
   • Der Klartext wird in Zeilenvektoren aufgeteilt mit Länge $n$, d.h. die HILL-Chiffre ist eine Block-Chiffre, bei der Blöcke fester Länge in einem Vorgang verschlüsselt werden.
3. Dechiffrierung
   • Dazu benötigt man die zu $M$ inverse Matrix, die wir $N$ nennen; diese erfüllt:
     $M \cdot N \equiv \mathbb{1}_{3 \times 3} \mod 26$

Notation: $\mathbb{1}_{3 \times 3} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix}$ (Einheitsmatrix)

Eigenschaften von Block-Chiffren

Eine wichtige Eigenschaft von Block-Chiffren ist die Diffusion (Shannon); d.h. die Änderung eines Klartextzeichens hat zur Folge, dass sich mehrere Chiffrezeichen ändern.

Diese Eigenschaft müssen heutige Block-Chiffren (DES, AES) aufweisen; dadurch wird die statistische Struktur von Klartextblöcken verschleiert.

Mathematische Grundlagen (kurz)

Relativ prime Zahlen

Definition: Zwei Zahlen $a, b \in \mathbb{Z}$ heißen relativ prim, coprim oder teilerfremd, falls sie keinen Primfaktor gemeinsam haben. Dies ist insbesondere dann der Fall, falls
$\text{ggT}(a, b) = 1$

gilt.

Totientenfunktion

Ein wichtiges Konzept ist die EULER-Funktion oder EULER-Totietennfunktion.

$\phi(n)$ gibt an, wieviele Zahlen $a \in \mathbb{N}, a \ge 1$ existieren mit $a < n$ und $\text{ggT}(a, n) = 1$

$\phi(n)$ gibt des Weiteren an, wieviele coprime Zahlen $< n$ existieren.

Es gilt: $\phi(p) = p - 1$, falls $p$ eine Primzahl ist.

Satz: Falls $\text{ggT}(m, n) = 1 \Rightarrow \phi(m, n) = \phi(m \cdot n)$

Folgerung: Wenn $p, q$ zwei Primzahlen sind und $n = p \cdot q$
$\Rightarrow \phi(n) = \phi(p \cdot q) = (p - 1) \cdot (q - 1)$.

Kleiner Satz von FERMAT

Falls $p$ eine Primzahl ist und $a$ eine positive ganze Zahl, die nicht durch $p$ geteilt wird, dann gilt
$a^{p - 1} \mod p \equiv 1 \mod p$

Der kleine Satz von FERMAT ist die Grundlage aller Primzahltests; diese prüfen (ohne zu faktorisieren), ob eine Zahl eine Primzahl ist oder nicht.

---

Falls für irgendwelche zufällig gewählten Zahlen $a$ der Ausdruck
$a^{p - 1} -a$

kein Vielfaches von $p$ ist, dann ist $p$ keine Primzahl.

---

RSA-Algorithmus

Mit diesen Werkzeugen kann man den RSA-Algorithmus durchbrechen.

Dieser lautet:

1. Man wähle zwei zufällige Primzahlen $p, q$ ($512, 1024, 2048, 4096$ Bit) und berechne
   $n = p \cdot q$

2. Berechne $\phi(n) = (p - 1)(q - 1)$.

3. Wähle ein $e$ mit $1 < e < \phi(n), \ \text{ggT}(e, \phi(n)) = 1$.

4. Berechne $d$ mit $e \cdot d \equiv 1 \mod \phi(n)$.

5. $K_{\text{pub}} = (e, n), K_{\text{priv}} = (d, n)$.

Verschlüsselung: $M$ geeignet als Zahl codiert $M < n$
$C = M^e \mod n$

Entschlüsselung:
$M = C^d \mod n$

DIFFIE-HELLMAN Key-Exchange Verfahren

Dieses Verfahren wurde in der Arbeit “New Directions in Cryptography” vorgestellt und zählt zu den Public-Key Verfahren, erlaubt aber

• keine Verschlüsselung
• keine digitale Signatur

Generell nutzen Public-Key Verfahren immer sogenannte Trapdoor-Funktionen; das sind Funktionen, die in der einen Richtung einfach sind, die Umkehrung jedoch schwierig bis unmöglich.

RSA: $p \cdot q \xrightleftharpoons[\text{schwierig}]{\text{einfach}} n = p \cdot q$

Eine andere Trapdoor-Funktion ist z.B.
$\rightarrow$ Berechne $\displaystyle \prod_{i = 1}^{11} \; (x - i ) = (x - 1) (x - 2) (x - 3) \ldots (x - 11)$
$\quad \qquad \qquad \qquad \qquad \ \ \, = x^{11} - 66x^{10} + 1925x^9 - 32670x^8$
$\quad \qquad \qquad \qquad \qquad \ \ \, \quad + 35742x^7 - 39916800x^6$

Das DH-Key-Exchange-Verfahren nutzt den diskreten Logarithmus als Trapdoor-Funktion; d.h. die Sicherheit des DH-Verfahrens hängt davon ab, dass es sehr schwierig (bis unmöglich) ist, diskrete Logarithmen zu berechnen.

Betrachte wieder die Menge $\mathbb{Z}_p = \{ 0, 1, \ldots, p - 1 \}$. Eine primitive Wurzel einer Primzahl $p$ ist eine Zahl in $\mathbb{Z}_p \backslash \{ 0 \}$, deren Potenzen alle Zahlen von $1$ bis $p - 1$ generiert. Ist $a$ eine primitive Wurzel, dann sind

$a \mod{p}, a^2 \mod{p}, a^3 \mod{p}, \ldots, a^{p - 1} \mod{p}$

alle unterschiedlich und bestehen aus den Zahlen $1$ bis $p - 1$ in irgendeiner (wilden!) Reihenfolge.

Das DH-Key-Exchange Kryptosystem

1. Szenario: Alice und Bob wollen einen gemeinsamen Schlüssel erzeugen, den nur sie kennen, ohne sich zuvor begegnet zu sein.
2. Alice und Bob einigen sich (öffentlich) auf eine Primzahl $q$ und eine primitive Wurzel $a$ ($(q, a)$ ist eine Art Public Key).
3. Geheimer Schlüssel Alice
   Alice wählt eine Zahl $X_A$ ($X_A < q$) und wird Alice benannt. Alice berechnet
   $Y_A = a^{X_A} \mod{q}$
   $Y_A$ geht an Bob.
4. Geheimer Schlüssel Bob
   Bob wählt eine Zahl $X_B$ ($X_B < q$) und wird Bob benannt. Bob berechnet
   $Y_B = a^{X_B} \mod{q}$
   $Y_B$ geht an Alice.
5. Alice berechnet $K = (Y_B)^{X_A} \mod{q}$.
6. Bob berechnet $K' = (Y_A)^{X_B} \mod{q}$.

$\rightarrow$ Da $K = K'$ (gleich), haben Bob und Alice einen gemeinsamen Sitzungsschlüssel.

ELGAMAL-Kryptosysteme (TAHER ELGAMAL, 1985)

Digitale Signatur

Schlüssel: Wähle eine Primzahl $p$ mit zwei Zufallszahlen $g, x$ mit $g, x < p$.
Berechne $y = g^x \mod{p}$

$K_{\text{pub}} = [y, g, p]$
$K_{\text{priv}} = [x]$

Signatur: $M$ soll signiert werden.
Wähle eine zufällige Zahl $k$, so dass $k$ und $p - 1$ coprim sind, d.h.
$\text{ggT}(k, p - 1) = 1.$

Berechne
$a = g^k \mod{p}.$

Berechne $b$ aus
$M \equiv (xa + kb) \mod{(p - 1)}$

Signatur: $(a, b)$, $k$ bleibt geheim.

Bob verifiziert die Signatur wie folgt:
Es muss gelten:
$y^a \cdot a^b \mod{p} \overset{!}{=} g^M \mod{p}$

Klartext, der von Alice signiert wird, ist $M = 10$.
Zum Signieren muss Alice die Zahlen $a, b$ bestimmen:

1. Alice wählt zufällige Zahl $k = 5$, ist ok: $\text{ggT}(5, 12) = 1$
2. $a = g^k \mod{p}$
   $\ \ \ = 7^5 \mod{13} \equiv 11 \mod{13}$
3. Berechne $b$ aus
   $M = (xa + kb) \mod{(p - 1)}$
   $10 = (3 \cdot 11 + 5 \cdot b) \mod{12}$
   $\quad \ = (9 + 5 \cdot b) \mod{12}$
   $\iff 1 \equiv 5 \cdot b \mod{12}$
   $\qquad \rightarrow \underline{b = 5}$

An Bob wird gesendet:

• Klartext $M$
• Signaturwerte $[a, b] = [11, 5]$
• $K_{\text{pub}}$ von Alice: $K_{\overset{A}{\text{pub}}} = [p = 13, g = 7, y = 5]$

Verifikation:
$\qquad \qquad (y^a \cdot a^b) \mod{p} \overset{!}{=} g^M \mod{p}$
$\text{links:} \quad \ \ \, (5^{11} \cdot 11^5) \mod{13} = 4 \mod{13}$
$\text{rechts:} \quad \ 7^{10} \mod{13} = 4 \mod{13}$
$\Rightarrow$ Beide Terme sind gleich.

Die FEISTEL-Chiffre

von HORST FEISTEL, ~1970 IBM

Die FEISTEL-Chiffre / oder FEISTEL-Netzwerk ist eine Vorlage / Muster für viele symmetrische Block-Chiffren, z.B.

DES, Blowfish, Twofish, CAST, RC5, MARS, ...

Bei der FEISTEL-Chiffre ist die Ver- / Entschlüsselung (fast) identisch, der Unterschied liegt lediglich in der Reihenfolge der Anwendung der sogenannten Rundenschlüssel.

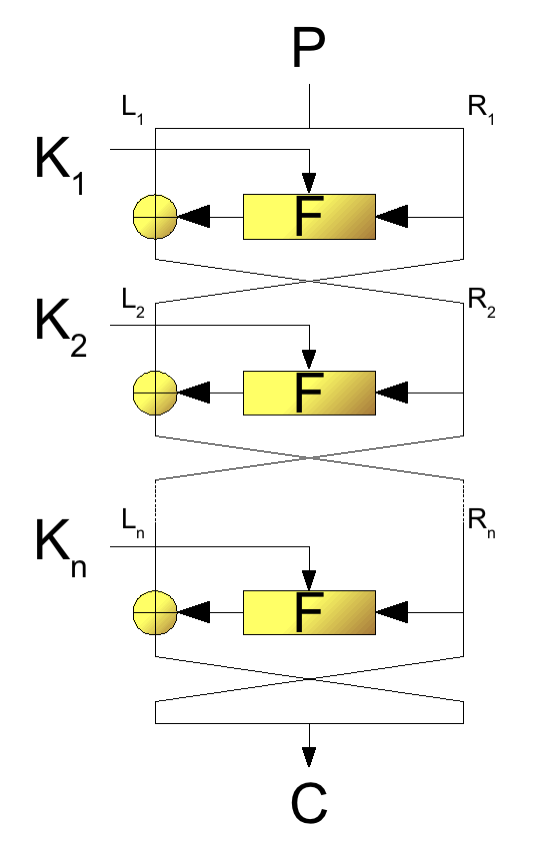
Abbildung 1: Aufbau eines Feistel-Netzwerkes (Quelle)

Betriebsmodi von Block-Chiffren

Jede Block-Chiffre kann in verschiedenen Arbeitsmodi eingesetzt werden (NIST FiPS PUB 81 und weitere)

• Electronic Code Book Mode (ECB)
• Cipher Block Chaining Mode (CBC)
• Cipher Feedback Mode (CFB)
• Output Feedback Mode (OFB)

Neu:

• Counter Mode (CTR)
• Galois Counter Mode (GCM) $\leftarrow$ eingebaute Authentifizierung

Electronic Code Book Mode (ECB)

Jedes $n$-Bit Klartextblock wird unabhängig von anderen mit dem gleichen Schlüssel $K$ verschlüsselt.

Abbildung 2: Verschlüsselung mittels ECB (Quelle)

Cipher Block Chaining Mode (CBC)

Input des Verschlüsselungsalgorithmus ist die XOR-Verknüpfung des letzten Chiffreblocks mit dem Klartextblock. Die Verkettung der Klartextblöcke mit den Chiffretextblöcken führt dazu, dass statistische Eigenschaften des Klartextes nicht auf das Chiffrat übertragen werden.

Abbildung 3: Verschlüsselung mittels CBC (Quelle)

CFB, OFB und CTR dienen dazu, eine Block-Chiffre als Strom-Chiffre zu betreiben.